Matematičko šibicarenje, 19. rujna 2021. godine
TAYLOROV RAZVOJ I "PREDVIĐANJE" PANDEMIJE
Ostanite sa mnom, ovo dugo traje, ali iskreno se nadam se da ćete nešto naučiti, ja sam se barem potrudio da tako bude.
Zamislimo igru u kojoj vam netko da niz brojeva, vrijednosti nečega po danima, recimo dnevnog broja novooboljelih od koronavirusa u nekoj zemlji, ili
visine dječaka iz mjeseca u mjesec. Taj netko vas nakon toga upita kolika bi vrijednost tog niza mogla biti u narednom periodu, tj. koliko bi npr. dječak
mogao narasti u iduća tri mjeseca ili koliki bi broj novozaraženih mogao biti u idućih nekoliko dana.
Pretpostavimo da je niz vrijednosti opisan nekakvom funkcijom, f(x), koja u svakoj vremenskoj točki (danu, mjesecu, ...) x daje vrijednost f(x), odn.
broj zaraženih ili visinu ili što nas već u konkretnoj situaciji zanima. Svi oni koji su imali kakvu-takvu matematiku na studiju sjetit će se
Taylorovog razvoja (ne bojte se velikih riječi, kako se nešto naziva uopće
nije ni važno) koji kaže da se bilo koja* funkcija f može jednostavno i približno zapisati oko neke točke a kao
f(x) = f(a) + f '(a)*(x-a),
gdje je x neki vremenski trenutak, npr. idući mjesec u rastu dječaka ili prekosutra u tijeku pandemije, a f(x) vrijednost funkcije u toj točki, odn. visina
dječaka idući mjesec ili broj novooboljelih od korone prekosutra. Točku a nazivamo točkom oko koje se funkcija razvija u red, a mogli bismo je nazvati i
točkom fiksacije. "Magični" broj koji vam za taj zapis treba je
f '(a)
koji se zove PRVA DERIVACIJA funkcije u točki a. Prvu derivaciju je pak lako
izračunati iz niza podataka koji ste dobili, odn. iz ponašanja niza poznatih vrijednosti u prošlosti. Prva derivacija je zapravo (linearizirani)
trend rasta ili pada funkcije.
Idemo sve to malo konkretizirati. Recimo da mjerimo visinu bebe nakon njenog rođenja (zapravo bi za bebice bolje bilo reći da mjerimo dužinu) i neka je ona
nakon prvog mjeseca bila 53.2 cm, a nakon drugog mjeseca 56.6 cm. Kolika će biti visina bebice nakon trećeg mjeseca?
Primjenjujući Taylorov razvoj na visinu bebice možemo zapisati
f(3) = f(2) + f '(2)*(3-2),
gdje je f(3) visina bebice nakon 3 mjeseca, f(2) visina bebice nakon dva mjeseca, a f '(2) prva derivacija visine bebice, odn. njen trend rasta izračunat
nakon dva mjeseca starosti. Ovaj se broj može jednostavno izračunati iz poznatih vrijednosti visine nakon prvog i drugog mjeseca starosti i to kao,
f '(2) = [f(2)-f(1)]/(2-1)
što daje f '(2) = (56.6 cm - 53.2 cm) / [1 mjesec] = 3.4 cm/mjesec. Ovo je zapravo TREND RASTA visine bebice izračunat na osnovi vrijednosti visine nakon prvog
i drugog mjeseca života i on nam kaže da se čini da bebica raste brzinom od 3.4 cm na mjesec (ovo ste i sami mogli izračunati bez ikakve ideje o Taylorovom
razvoju funkcije - nakon drugog mjeseca je beba bila viša za 3.4 cm nego nakon prvog mjeseca starosti, što znači da beba raste 3.4 cm na mjesec). Znajući sada
trend rasta, izračunat nakon dva mjeseca (a=2), to nam omogućuje da "predvidimo" vrijednost visine bebe nakon trećeg mjeseca, i to kao
f(3) = 56.6 + 3.4 * 1 = 60 cm.
Nema u ovome nikakve pameti, pretpostavili smo da će trend rasta visine bebe i u trećem mjesecu biti jednak kao i ranije, tj. da će bebica porasti za još
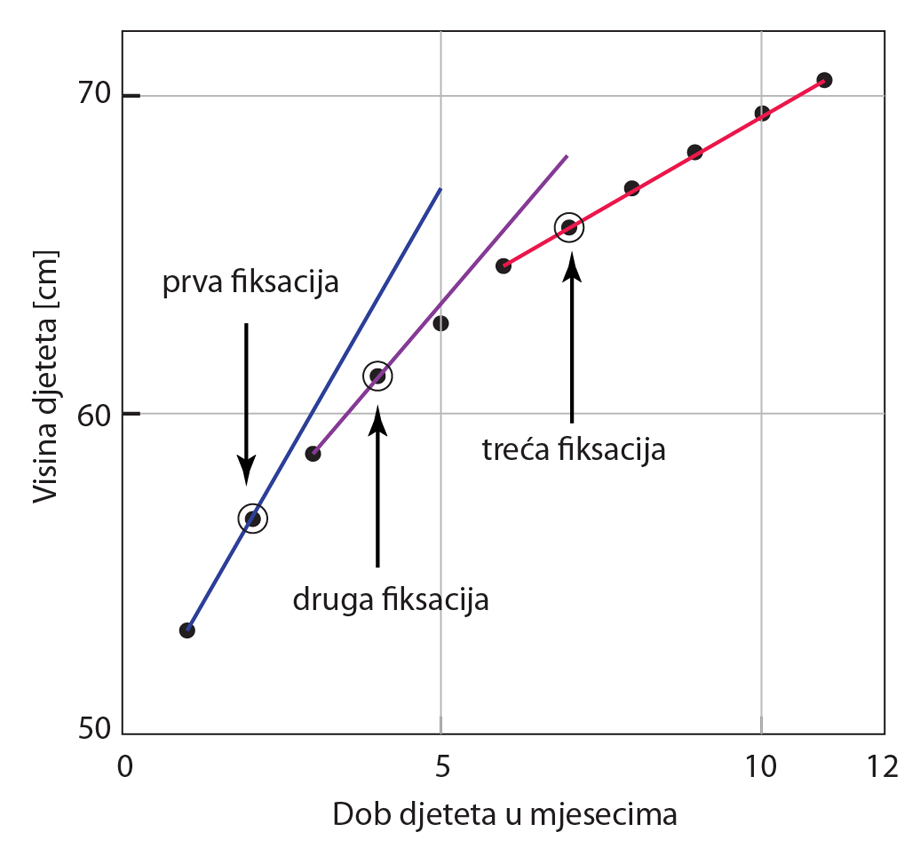
3.4 cm na godinu do ukupno 60 cm visine. Ovo je "predviđanje" prikazano plavom linijom na slici u ovom postu koja prikazuje pravac izračunat iz dvije točke mjerenja,
odn. visina bebice nakon prvog i nakon drugog mjeseca starosti. Kad je prošlo tri mjeseca, bebi smo izmjerili visinu i ustanovili da je ona visoka 58.7 cm, dakle
manje nego što smo predvidjeli, što znači da je bebica sporije rasla nego u mjesecima ranije. No, pogreška od 1.3 cm i nije tako velika pa bismo mogli
inzistirati na našem modelu fiksiranom nakon dva mjeseca rasta bebice i potjerati ga i na četvrti mjesec rasta bebice (naprosto slijedimo plavu liniju
koja predstavlja "model" fiksiran nakon dva mjeseca rasta). Primjenom Taylorovog razvoja za datum u daljoj budućnosti, za visinu bebice nakon 4 mjeseca dobili
bismo
f(4) = f(2) + f '(2)*(4-2)
odn. f(4) = 56.6 + 3.4 * 2 = 56.6 + 6.8 = 63.4 cm.
Nema u ovome opet ništa pametno, tvrdoglavo inzistiramo na ideji da trend od 3.4 cm godišnjeg rasta opisuje razvoj naše bebice (da je rast opisan plavom
linijom) pa će ona za dva mjeseca od zadnjeg mjerenja porasti za 6.8 cm. Pričekamo li da prođe 4 mjeseca i opet izmjerimo visinu bebice dobivamo da je ona 61.1 cm.
Sad smo pogriješili još više u svojoj procjeni i to za 2.3 cm, što opet i nije tako loše, no teško bi se moglo reći da smo "pogodili muhu u letu". No, pretpostavimo
da smo tvrdoglavi u svojoj namjeri da koristimo raniju fiksaciju rasta (odn. "modela rasta") izračunatu nakon dva mjeseca rasta bebice i da je primijenimo
na visinu bebice nakon 5 mjeseci. Naše bi predviđanje tada bilo
f(5) = f(2) + f '(2)*(5-2)
odn. f(5) = 56.6 + 3.4 * 3 = 66.8 cm.
Dakle, 3.4 cm rasta po mjesecu, nakon tri mjeseca (od drugog mjeseca rasta) to je još 10.2 cm, odn sveukupno 56.6 + 10.2 = 66.8 cm. No, mjerenje nam daje da je
visina bebice nakon 5 mjeseci tek 62.8 cm. Ovaj put smo promašili još i više i to za puna 4 cm visine. Očito je da naš "model" sve slabije radi kako vrijeme
odmiče, i to naprosto zato što se trend rasta visine bebice smanjio, tj. bebica sporije raste kako stari. Ovoliko bi odstupanje pokolebalo i najuvjerenijeg
prognozera, no ono što bi on mogao učiniti je da naprosto ponovno izračuna trend rasta, ali u kasnijoj vremenskoj točki odn. da fiksira svoje
predviđanje u kasnijem intervalu.
Ako bi odlučio fiksirati "model" nakon četiri mjeseca rasta (tj. sad uzima da je a=4 umjesto a=2), dobio bi da je novi trend rasta
f '(4) = [f(4)-f(3)]/(4-3) = (61.1 - 58.7) / 1 = 2.4 cm/mjesec ,
dakle manji nego što je izračunao ranije, a to se jasno vidi iz eksperimentalnih podataka kojima se rast usporava s odmakom vremena. Ovaj bi novi trend rasta
naš prognozer onda mogao ubaciti u Taylorov razvoj da dobije
f(5) = f(4) + f '(4)*(5-4) = 61.1 + 2.4 * 1 = 63.5 cm
Novo "predviđanje" (63.5 cm) je puno bolje od ranijeg predviđanja (66.8 cm) fiksiranog u ranijoj točki rasta i promašuje za 0.7 cm umjesto za puna 4 cm
visine. Nova je fiksacija "modela" (ljubičasta linija na slici) dakle dala točnije predviđanje, no u suštini se radi samo o tome da smo primijetili da se
trend rasta bebice smanjuje kako vrijeme odmiče pa samo samo umjesto ranije procjene od 3.4 cm na osnovu novijih podataka procijenili da će rast biti tek 2.4 cm
mjesečno. Nastavljajući u istom duhu, "prognozer" predviđa na osnovu novofiksiranog modela da će bebica nakon 6 mjeseci biti visoka
f(6) = f(4) + f '(4)*(6-4) = 61.1 + 2.4 * 2 = 65.9 cm,
no mjerenje pokazuje 64.6 cm, dakle prebacio je za 1.3 cm jer trend ili brzina rasta bebice i dalje usporava kako vrijeme odmiče. Tip je tvrdoglav, i inzistira
na novofiksiranom modelu (slijedi ljubičasti pravac na slici) pa za visinu nakon 7 mjeseci predviđa
f(7) = f(4) + f '(4)*(7-4) = 61.1 + 2.4 * 3 = 68.3 cm,
a mjerenje daje 65.9 cm, odn puna 2.4 cm manje. U ovom se trenutku naš prognozer opet pokoleba pa odluči ponovno fiksirati model, ovaj put u točki nakon
6 mjeseci rasta, pa izračuna novi trend (prvu derivaciju)
f '(6) = [f(6)-f(5)]/(6-5) = (64.6 - 63.5)/1 = 1.1 cm/mjesec,
što znači da je trend (brzina) rasta još manji nego što je ranije, svega 1.1 centimetar mjesečno. Njegova opetovana fiksacija "modela" u kasnijoj vremenskoj točki bi za visinu
nakon 7 mjeseci dala
f(7) = f(6) + f '(6)*(7-6) = 64.6 + 1.1 * 1 = 65.8 cm,
što je ovaj put tek 0.1 cm manje od izmjerene visine bebice. Hej, pa to je odlično, nije baš kao da si pogodio muhu u letu, ali je sasvim pristojno! Naš
prognozer s probuđenim optimizmom predviđa s NOVOFIKSIRANIM TAYLOROVIM RAZVOJEM (crvena linija na slici) i dalje, pa za visinu nakon 8 mjeseci predviđa
f(8) = f(6) + f '(6)*(8-6) = 64.6 + 1.1 * 2 = 66.8 cm,
i nestrpljivo očekuje da prođe još jedan mjesec rasta djeteta kad izmjeri visinu od 66.9 cm. HEJ, HEJ! Pa to je BRUTALNO, idemo dalje! Za visinu nakon 9 mjeseci
dobiva
f(9) = f(6) + f '(6)*(9-6) = 64.6 + 1.1 * 3 = 67.9 cm,
dok mjerenje visine djeteta nakon 9 mjeseci daje 68.0 cm. HEJ, HEJ, HEJ! Pa to je fantastično, pogodio je muhu u letu, puna tri mjeseca nakon fiksacije
svog "modela rasta", on i dalje promašuje za jedva 0.1 cm, idemo dalje. Nakon 10 mjeseci, sve sigurniji prognozer predviđa da će dijete biti visoko
f(10) = f(6) + f '(6)*(10-6) = 64.6 + 1.1 * 4 = 69.0 cm,
dok mjerenje daje 69.2 cm. Odlično! Promašio je samo za 2 milimetra, no njemu je sad sve jasno, jer on već od šestog mjeseca zna kolika će biti visina
djeteta nakon devet mjeseci i s novostečenom odlučnošću za jedanaesti mjesec predviđa f(11) = 70.1 cm (ovo izračunajte sami, sad je sve već valjda potpuno jasno),
dok mjerenje daje upravo 70.1 cm. Naš prognozer trijumfira i za sebe počinje tvrditi da je ekspert za rast djece.
No, svatko tko je do ovdje pratio argument može zaključiti da je "prognozer" zapravo najobičniji prevarant jer koristi elementarnu matematiku ekstrapolacije za
"predviđanje budućnosti". On time može oduševiti jedino one koji ne znaju mnogo ni o geometriji (tj. povlačenju pravca kroz dvije točke) ni o matematici te im se
može učiniti da čovjek uistinu nešto predviđa. Sve što on u stvari radi je najobičnija ekstrapolacija trenda rasta funkcije i to iz
podataka o proteklom rastu koji su mu dostupni. No, naš ekspert zapravo nema pojma kako beba raste niti zašto je rani rast bebe, u prva dva-tri
mjeseca bio brži nego kasniji rast, nakon 6-7 mjeseci rasta. On nema pojma o biologiji, metabolizmu, hormonima, pubertetu, razlici između muške i ženske djece,
ni o čemu nema pojma, on zna tek malo jeftine matematike kojom vara naivne roditelje. Ne samo to, on čak ne može reći ni hoće li se rast djeteta zaustaviti
i kad jer ne zna zapravo ništa osim elementarne matematike.
Ključno je za "kvalitetu" njegove "prognoze" da nanovo fiksira model kad god primijeti da se trend rasta promijenio. U ovom primjeru prognozer je to
radio tri puta, no najlošije je prošao s prvom fiksacijom kad se trend rasta naglo usporavao. Da je bio tvrdoglav, i ostao pri prvoj fiksaciji, za
visinu djeteta nakon 11 mjeseci bi dobio f(11) = f(2) + f '(2) * (11-2) = 56.6 + 3.4 * 9 = 87.2 cm, tj pogriješio bi za punih 17.1 cm! No, naš je matematičar
pravodobnim ponovnom fiksacijama "modela" poboljšavao svoja "predviđanja", a nakon 6 mjeseci dobio odlične rezultate i "predvidio rast" vrlo, vrlo točno
u idućih 5 mjeseci! Zašto? Zato što se TREND RASTA NIJE UOPĆE PROMIJENIO u tih 5 mjeseci (kažemo da je funkcija približno linearna), iako naš prognozer nema
pojma ZAŠTO, jer on zapravo ništa ne zna ni o djeci ni o rastu organizama ni o biologiji, on zna tek malo elementarne matematike kojom hipnotizira naivne
roditelje koji bi jako htjeli znati koliko će njihovo dijete porasti. On mudro drži fige da se nepromjenjljiva stopa rasta nastavi i u budućnosti kako bi
njegova predviđanja s ranom fiksacijom bila točna, iako nema blage veze hoće li tako uistinu i biti. Zapravo, sam fizikalni (stvarnosni) sadržaj točaka za njega
je potpuno irelevantan, i njegov se "model" podjednako može odnositi na temperaturu kade napunjene vodom ili nagib kosog tornja u Pisi. Kad tvrdi da o bilo kojem
o tih fenomena nešto sa sigurnošću zna on zapravo postaje najobičniji MATEMATIČKI ILUZIONIST i šibicar.
Za one koji žele znati više:
Skup podataka za visinu djeteta koji sam prikazao dolazi iz knjige On Growth and Form (O rastu i obliku), jedne od mojih omiljenih knjiga koju je napisao genijalni škotski zoolog širokog obrazovanja, D'Arcy Thompson. Mjerenja visine pariške muške djece je načinio M. M. Variot i objavio davne 1907. godine u časopisu The American Naturalist. Kvantifikacija rasta je stara opsesija agronoma, biologa, zdravstvenih djelatnika, a da o ekonomistima i mešetarima i ne govorimo.
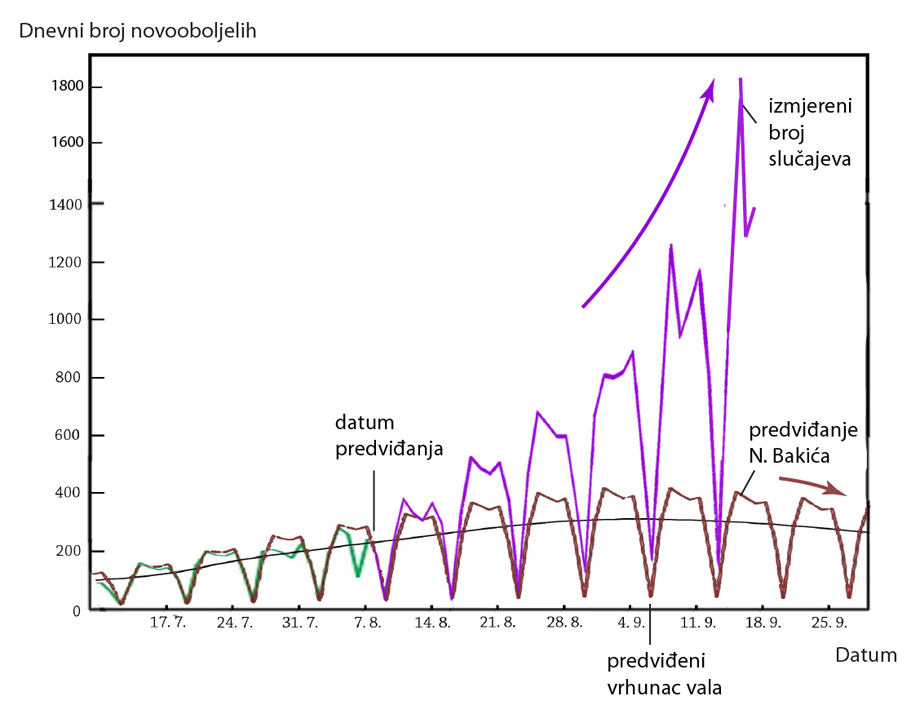
Ljudi bez matematičkog obrazovanja često su impresionirani trikom koji sam opisao, a kod nas je to slučaj otkad traje ova pandemija gdje imamo razne matematičke proroke koji navodno modeliraju tijek pandemije. Svojstvo je tih njihovih prognoza da svako malo (čim bude "gusto") promijene točku fiksacije "modela", upravo kako je i opisano u tekstu. Oni tako vrijedno iznose novo "predviđanje" svako malo i po potrebi, no rijetko ponude i predviđanje za datum i veličinu maksimuma vala, jer njihova "predviđanja", naravno, redovito promašuju u bilo čemu što bi moglo biti uistinu korisno i što je lako provjerljivo. To je stari iluzionistički trik, a zašto je maksimum teško predvidjeti iz jeftinih ekstrapolacija trebalo bi biti jasno iz gornjeg pojašnjenja. Takvim se metodama maksimum vala može "predvidjeti" u trenutku kad svi, bez ikakve matematike, vide da je maksimum vala tu negdje. Nema boljih argumenata za takve upravo od matematike, a slika ispod prikazuje stvarne podatke o razvoju pandemije u Hrvatskoj i predviđanje jednog prognozera koji je imao nesreću da svoj model fiksira u nezgodnoj točki (ispod) kad je došlo do nagle promjene trenda, a omaknulo mu se i da ponudi predviđanje za maksimum i magnitudu vala. Nakon ove moje javne objave, dotični je prognozer na mene pokrenuo čitavu hajku na društvenim mrežama.
* Za one koji glume matematičke eksperte, poput našeg matematičara, ono "bilo koja" funkcija je skaredno, jer postoje patološke funkcije koje nemaju Taylorov razvoj ili imaju razvoj koji se patološki ponaša. Takve funkcije redovito ne nalazimo u prirodnim fenomenima, a pogotovo ne u mjerenjima rasta organizama ili broja zaraženih.
| << Zastajem | Vlado, Hrvat >> |
Zadnji put osvježeno: 19. rujna 2021. godine.