Kolaps membrana (15. listopada 2010. godine)

Često se iznenadim čitajući stare članke koji se bave uglavnom klasičnom fizikom i problemima od nekog "praktičnog" značenja. Dok sam radio na članku >> Stabilnost elastičnih ikozadeltaedarskih ljusaka izloženih jednolikom vanjskom tlaku: Primjena na viruse izložene osmotskom tlaku (prijevod naslova) načitao sam se takvih starih radova koji su se bavili uglavnom kolapsom podmornica i batiskafa pod hidrostatskim tlakom (u dubini). Dio tih radova nikad nije ni objavljen u "standardnoj" znanstvenoj literaturi nego su ostali kao izvješća za potrebe američke vojske. "Stara" fizika je redovito ozbiljna i temeljita, autori su morali u promišljanju sistema otići mnogo dalje nego danas kad nam već u ranoj fazi pomaže računalo. Nekad je takve radove teško pratiti, a s današnjeg stanovišta, neke od razvijenih procedura su i nepotrebne.

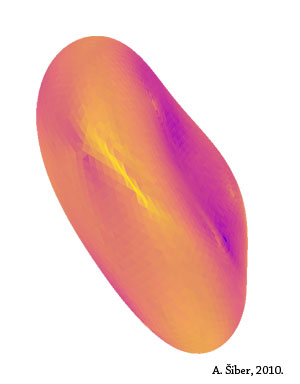
Problem kolapsa struktura pod tlakom je realan primjer >> fizike katastrofe koja opisuje sustave čija se svojstva naglo promijene u kritičnim uvjetima, samo malom promjenom nekih od parametara sustava. U konkretnom slučaju, primjenom tlaka ljuska ("podmornica") se deformira i odupire se vanjskom tlaku promjenom oblika - takva je situacija (prije kolapsa ljuske) prikazana na slici koja je otvorila post (gornji lijevi kut). No, na nekom kritičnom tlaku (tlaku na kojem sistem postaje nestabilan i podložan kolapsu) ljuska se ne može više deformirati malim pomacima svoje površine nego se naglo uruši. Kolaps može biti potpun, tj. ljuska ostaje posve zgnječena, a može biti i djelomičan gdje ljuska nalazi neko novo stabilno stanje tj. neki novi deformirani oblik koji se dalje odupire promjenama tlaka malim deformacijama.

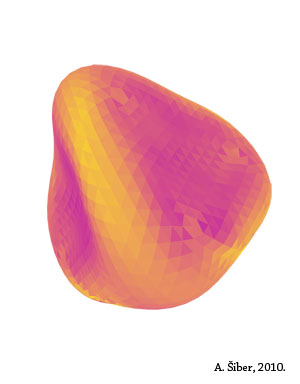
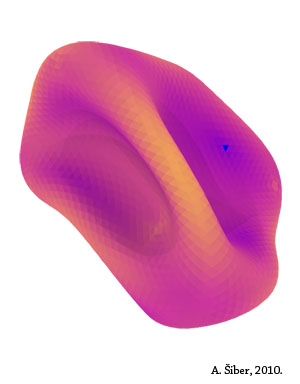
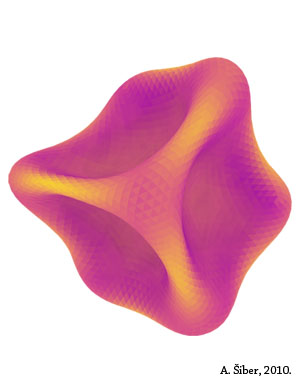
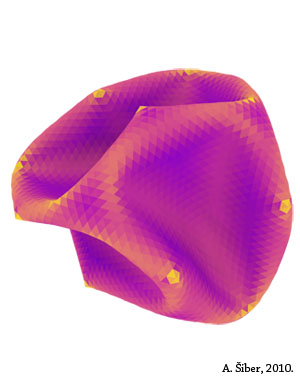
Kako točno izgleda kolapsirani oblik teško je pitanje, ali sam na njega djelomično odgovorio u članku. Ovisno o parametrima elastičnosti sustava, ljuske kolapsiraju na različite načine, a neke globalne karakteristike urušene strukture su sačuvane i ovisne samo o jednom broju koji se u teoriji ljusaka naziva Foppl-von Karmanov broj. U svakom slučaju, i ovo istraživanje je proizvelo zanimljivu slikovnost koju možete vidjeti na slikama koje nudim. Različite slike su kolapsirani oblici dobiveni za različita elastična svojstva ljuske.

Boje na slikama imaju konkretno značenje: žuti dijelovi površine pohranjuju mnogo elastične energije, a ljubičasti malo. Zato je ljuska žuta na pregibima i naglim motanjima svoje površine.

<< Igra staklenim perlama

Driving to Gogo >>

Zadnji put osvježeno 15. listopada 2010. godine