Vanzemaljske školjke

Vanzemaljske školjke, 19. rujna 2011. godine

Lako je matematički konstruirati kakvog jednostavnog puža ili školjkicu (slika iznad). Njihova struktura da se jednostavno zapisati u obliku kompaktne formule. Radi se o spirali u tri dimenzije. Mnogo je teksta napisano o ovoj "formuli za školjke". Tako npr. D'Arcy Thompson u svom kapitalnom djelu "On growth and form" (O rastu i obliku) u XI, XII i XIII poglavlju govori o svojstvima (logaritamske) spirale te o školjkama i rogovima, čiji se oblik može zapisati na sličan način kao i oblik školjaka. Thompsonov tekst bio je inspiracija mnogim kasnijim istraživačima (vidjeti npr. reference [1-5]). Meni su od većine matematičkih pokušaja da se opiše "točan" izgled školjaka zanimljivije Haeckelove prekrasne ilustracije školjaka. Ispod je prikazana ilustracija broj 44 iz Haeckelove knjige "Kunstformen der Natur" na kojoj on prikazuje (vjerojatno opet pretjerano stilizirano, vidi moj >> prethodni post o Ernstu Haeckelu) razne amonite, izumrlu skupinu morskih beskralježnjaka.

Ako se oblik školjke želi opisati dovoljno detaljno, onda se formule znatno kompliciraju. Slika ispod prikazuje formule koje u svom predavanju / MatLab GUI tutorialu iznosi Joceline Lega, a sve prema radovima M.B. Cortiea. Za relativno male efekte u obliku školjke potrebno je uvoditi znatne komplikacije u "opću formulu" za školjke koja time postaje sve manje kompaktna.

Na naslovnoj stranica Doverovog reprinta kompletnog izdanja Thompsonove knjige nalazi se prekrasna ilustracija / fotografija spirale i to u školjki Nautilusa. Mene je to inspiriralo za četvrto poglavlje moje knjige >> "Problem promatrača" u kojemu je D'Arcy Wentworth Thompson glavni lik. Samo za čitatelje "Konstrukcije stvarnosti" nudim >> download tog poglavlja. Na slici ispod prikazana je ilustracija na kraju IV. poglavlja, a navod ispod ilustracije prenesen je iz knjige i mislim da je zanimljiv u kontekstu fizikalne nužnosti i matematike oblika o kojoj Thompson često diskutira.

Sutradan je D'Arcy Thompson krenuo u svoju uobičajenu šetnju uz zaljev Svetog Andrije prekapajući usput po školjkama i puževima koje je more izbacilo na obalu. Ništa posebnog nije bilo. Uglavnom Buccinum undatum. Pokoji Vertigo geyeri je bio najveće uzbuđenje na koje je naišao. Školjke Sjevernog mora tako su dosadne u usporedbi sa sjajnim primjercima iz tropskih mora i koraljnih grebena. Na klupici uklesanoj u stijenu iz džepa je izvadio sjajni primjerak ljuske malenog Nautilus macromphalusa iz Nove Kaledonije, dijametra svega dvanaest centimetara. Skoro da je osjetio toplinu iz prelijepog komada organskog materijala. Na zimskom svjetlu gladnog i sivog grada na Sjevernom moru, njegova slojevita struktura stvarala je suptilni spektar duginih boja kako ga je Thompson s divljenjem okretao u rukama.

„Prekrasan komadić evolucije. Živi fosil. Ali kako je to nastalo... I to tako pravilno. Otkud dolazi sva ta matematika, logaritamska spirala? Čudno je to. U toj spiralnoj ljusci vidi se fenomen rasta u svojoj punoj matematičkoj jednostavnosti, neometan sporednim efektima. I ta spirala je iznad života samog. Ona je nekakav princip, razumni i matematički temelj života i svemira. Jer isti je spiralni uzorak u različitih vrsta, u vrlo raznolikim vrstama gastropoda i cephalopoda. Pa čak i izvan razreda mekušaca, među ameboidnim ljuskastim foraminiferama, ali i crvima spirorbisima, spirographisima i ditrupama. I ne samo danas i ovdje ... Nego i milijunima godina prije. U fosilima ammonitoida. Pa čak i ovi neugledni Buccinumi kriju formulu istog sveprisutnog spiralnog dizajna, samo skromnijeg. Ne radi se tu samo o evoluciji, tu se radi o nečem mnogo dubljem. O neizbježnosti oblika i povezanosti svega živoga i neživoga. Jer i ono što je živo i ono što je neživo mora udovoljavati istim zakonima fizike. A zakoni fizike su matematički. Eto, zato je to tako. Da...“

Thompson je sad već zadovoljno klimao glavom. Svejedno, nešto je u svemu tome nedostajalo.

„Ali ... Što točno znači da je život uređen prema matematičkim i fizikalnim zakonitostima? Znači li to da iza cijelog svemira stoji razum sličan našem čije namjere zato i možemo pojmiti ili da su matematika i fizika ništa više nego samo najbolji način na koji se silna raznolikost Univerzuma može najjednostavnije uklopiti u materijalno ustrojstvo ljudskog mozga? Možda se radi samo o bijednom i nečistom rezonantnom zvuku raštimanog glazbala, zvuku koji zovemo matematikom. Možda ničeg dubljeg u tome nema. Matematika kao rezonanca ove sive moždane tvari koja izvan same te tvari ima sasvim skroman i bitno ograničen smisao. Način na koji opisujemo ne prirodu kakva jest, nego samo naše znanje o njoj... Unosi li matematičar ili priroda sama matematiku u filozofiju prirode? Na kraju... nije ni važno. Štogod to bilo još uvijek je hrabro. Svaka znanost bi trebala, slijedeći najbolji primjer fizike, tražiti odgovore na velika pitanja i teorije koje ne objašnjavaju samo pojedinačno nego premošćuju velike udaljenosti i povezuju naizgled sasvim različito. Jer kvaliteta znanosti se mjeri jedino prema njenoj povezanosti s matematikom. Pa čak i ako na kraju zaključimo da zurimo u same sebe, vrijedilo je probati. Nema nikakve koristi od davanja imena stvarima.“

Spirala kao element dizajna školjaka nije uvijek očigledna kao u slučaju Nautilusa. Vidi se to i iz Haeckelovih ilustracija >> Prosobranchia na slici iznad. Umjesto traženja formule koja opisuje školjku puno je korisnije, a i fizikalnije kodirati efektivni algoritam rasta školjke. Iz kodiranja jednog takvog algoritma rasta nastale su originalne ilustracije koje predstavljam u ovom postu.

Kao alternativa traženju jednadžbe za površinu školjke, školjku je moguće predstaviti i kao niz objekata u prostoru, npr. sfera i cilindara koji su u prostorne odnose dovedeni (vremenskim) procesom rasta. No, takvi objekti su i dalje diskretan skup pa ih je potrebno "uklopiti", "spojiti" u jedan, glatki objekt školjke. U računalnoj grafici postoje posebno pogodni objekti za takve potrebe koji se nazivaju metaballs ili blobs. Ideja je da se svakoj točki u prostoru (npr. svakom centru sfere) pridruži skalarno polje koje trne s udaljenošću od centra. Ukupno polje skupa točaka je suma svih pojedinih polja, a blob objekt je izo-površina takvog polja, tj. površina na kojoj je vrijednost ukupnog polja zadana. Detalji metaballs konstrukcije mogu se pronaći u članku Jamesa Blinna [6], a ja sam je sa svojim koautorima, Anže Lošdorferom Božičem i Rudijem Podgornikom koristio u članku koji smo nedavno završili, a kojeg za sad možete >> downloadirati s arXiva (Energies and pressures in viruses: contribution of nonspecific electrostatic interactions). Mi smo željeli prikazati distribuciju naboja u virusnim omotačima, no kako su naboji diskretni, niz točaka u 3D baš i ne daje neki uvid i osjećaj za raspodjelu naboja. U tu svrhu smo i koristili blobove i to u Povray implementaciji.

Vratimo se školjkama. Kad jednom kodiramo proces rasta i odredimo način na koji povezujemo diskretni skup točaka (blobs), ostaje nam da testiramo algoritam. Naravno, moguće je pokušati kreirati neku "stvarnu" školjku, tj. štimati prametre algoritma sve dok se ne dobije dobro slaganje s postojećom strukturom. Ovo je i suština mnogih prethodnih radova o matematičkoj konstrukciji školjaka (vidi npr. [4]), a jedan moj takav pokušaj prikazan je na slici iznad.

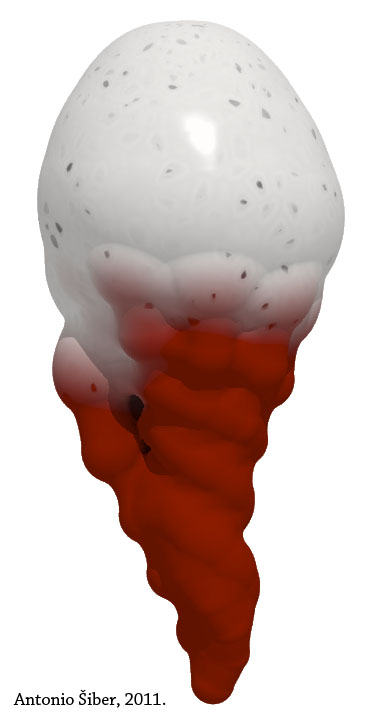
Ali, kad već kodirate "stvarnost", nema potrebe da se zadržite na jednoj od njenih realizacija. Konstruirajmo (alternativnu) stvarnost! Tako "školjka" iznad predstavlja zanimljivu konstrukciju baziranu na "algoritmu za školjke", ali potpuno nevezanu na neku "stvarnu" školjku. Moja dvogodišnja nećakinja u slici uopće nije prepoznala školjku ili pužića nego mi je lijepo kazala da je to sladoled! Školjka-sladoled.

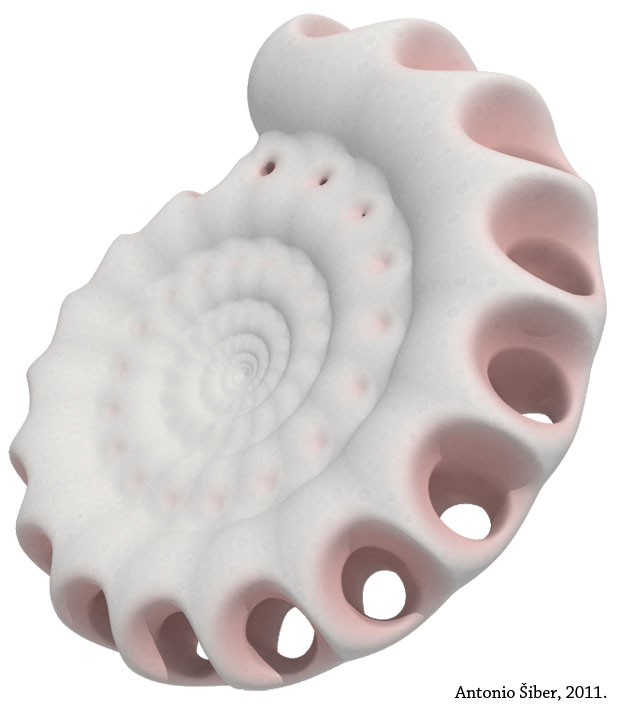
A na slici iznad prikazana je još jedna konstrukcija koja pomalo liči na amonite, ali je zanimljiva zbog dodatnih elemenata, otvora na strukturi školjke. Zamislite ovu sliku otisnutu na 150 x 150 cm i postavljenu iznad kamina. Ružičasta boja mogla bi se lako izmijeniti tako da bude žućkasta ili zelenkasta pa čak i plava, u skladu s drugim elementima dizajna u zamišljenoj dnevnoj sobi.

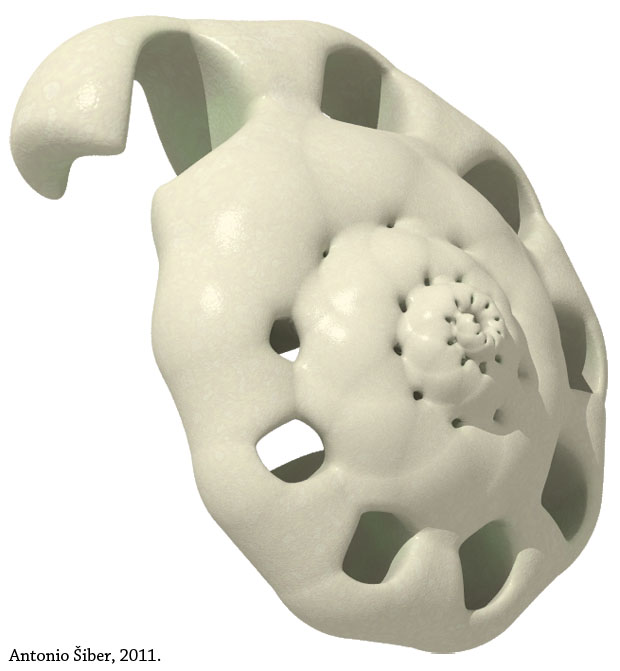
Slična, a opet malo drukčija konstrukcija prikazana je na slici iznad. Radi se o istoj "školjki" promotrenoj odozgo i odozdo.

Na slici iznad prikazana je vjerojatno najneobičnija i najneprepoznatljivija školjka koju sam konstruirao. Moj nećak Ivor je u njoj vidio "kamenčić", ali algoritam koji se nalazi iza konstrukcije ovog objekta isti je kao i onaj koji je iskorišten za konstrukciju slike koja je otvorila ovaj post, dakle svima prepoznatljivog pužića.

I na kraju, želim vas podsjetim ako ste zaboravili:

1) >> OVDJE možete downloadirati četvrto poglavlje "Problema promatrača", a
2) >> OVAJ vas link vodi na nedavno završeni rad o elektrostatici virusa postavljen na arXiv.

LITERATURA :

[1] K. Jirapong and R.W. Krawczyk, Seashell Architectures, ISAMA/Bridges 2003 Conference, Mathematical Connections in Art, Music, and Science, Granada University, Spain, July, 2003.

[2] J. Picado, Seashells: The plainness and beauty of their matehmatical description, Loci (March 2009), DOI: 10.4169/loci003294

[3] D.R. Fowler, Hans Meinhardt and Przemyslaw Prusinkiewicz, Modeling seashells, SIGGRAPH '92, Proceedings of the 19th annual conference on Computer graphics and interactive techniques, ACM New York, NY, USA, 1992

[4] C. Galbraith, P. Prusinkiewicz and B. Wyvill, Modeling Murex Cabritii Sea Shell with a Structured Implicit Surface, CGI '00, Proceedings of the International Conference on Computer Graphics IEEE Computer Society Washington, DC, USA, 2000.

[5] C. Illert, Formulation and Solution of the Classical Seashell Problem. II Tubular Three-Dimensional Seashell Surfaces, Il Nuovo Cimento 11 D (5), 761 (1989).

[6] J.F. Blinn, A Generalization of Algebraic Surface Drawing, ACM Transaction on Graphics, 1 (3), 235 (1982).

<< Glazba za banane

Kaustika Brune Pauna >>

Zadnji put osvježeno: 19. rujna 2011. godine.