Membrane collapse (15th od October 2010)

I often get surprised while reading old papers that deal with classical physics and problems of some "practical" meaning. While I was working on a paper >> Stability of elastic icosadeltahedral shells under uniform external pressure: Application to viruses under osmotic pressure I read quite some number of such old papers that dealt mostly with collapse of submarines and batiscaphs under hydrostatic pressure (submerged). Part of those papers was never published in "standard" scientific literature but remained in the form of reports for the needs of American military. "Old" physics is typically serious and thorough, the authors had to go a lot farther in their understanding of the system than we need to today when we can use computers in the early stage of research. Sometimes it is difficult to follow these works, and from the standpoint of today, some of the developed procedures are no longer necessary.

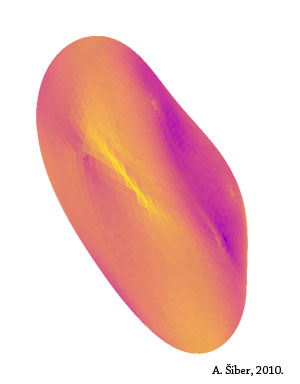
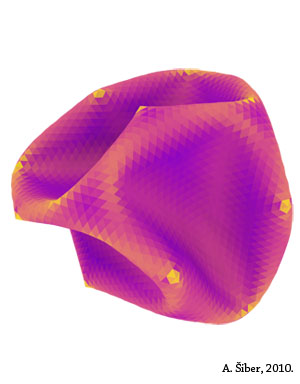
The problem of collapse of structures under pressure is a real-world example of >> catastrophe theory which describes systems whose properties suddenly change in critical conditions, only by a small change in some of the system parameters. In the case at hand, when the pressure is applied, the shell ("submarine") becomes deformed and resists further increase in pressure by its changed shape - such a situation is shown in the top-left corner in the image that opened the post. But, at some critical pressure (the pressure at which the system becomes unstable and prone to collapse), the shell can no longer deform by small changes of the shape of its surface and it suddenly collapses. The collapse can be complete, i.e. the shell remains completely "squashed", or it can be partial and the shell finds some new stable state i.e. some new deformed shape that can again resist the pressure by slightly deforming.

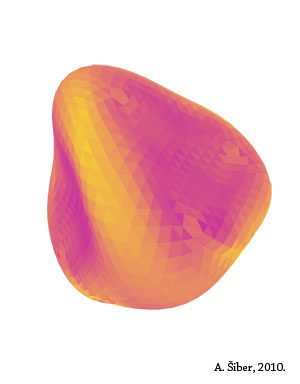
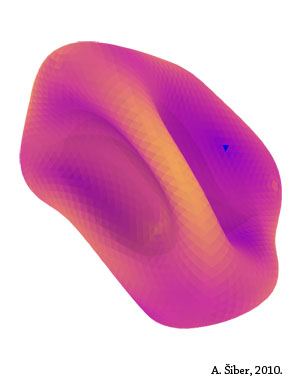
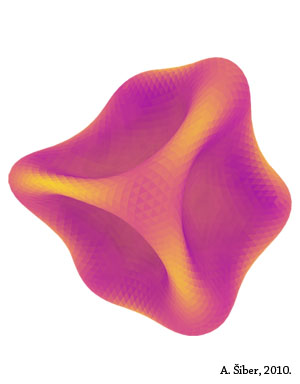
The question of exact shape of the collapsed shell is a tough one, but I answered to it partially in the paper. Depending on the elasticity parameters of the system, the shells collapse in different manners and some global characteristics of the collapsed structure are preserved and they depend on a single parameter that is called Foppl-von Karman number in the theory of shells. In any case, this research has also produced interesting imagery that you can see on the page. The different images are collapsed shapes obtained for different elastic properties of the shell.

Colors in the images have a fixed meaning: yellow parts of the surface contain a lot of elastic energy and the violet ones do not. That is why the shell is yellow in places where its surface curves.

<< The glass bead game

Driving to Gogo >>

Last updated on 15th of October 2010. godine