Alien seashells, 19th of September, 2011.

It is easy to mathematically construct some simple snail or a seashell (the image above). Their structure can be easily written down in a form of a compact formula based on a three-dimensional spiral. A lot of text has been written regarding this "formula for seashells". For example, D'Arcy Thompson in his kapital work "On growth and form" in Chapters XI, XII and XII writes about properties of (logarithmic) spiral and on seashells and horns, whose shape can be written down similarly as the shape of seashells. Thompson's text was an inspiration for many researchers that came later (see e.g. references [1-5]). To me, Ernst Haeckel beautiful illustrations of shells are more interesting than most of the mathematical attempts to describe an "exact" shape of seashells. On the image below I show an illustration No. 44 from Haeckel's book "Kunstformen der Natur" in which he shows (probably over stylized, see my >> earlier post on Ernst Haeckel) different sorts of ammonites, extinct group of sea invertebrates.

If one insists on describing the shape of seashell in sufficient details, then the formulas complicate significantly. The image below shows the formulas that Joceline Lega used in her lecture / MatLab GUI tutorial, based on the works of M.B. Cortie. To get relatively subtle effects in the seashell shape one needs to introduce complications in the "general formula" for seashells which becomes much less compact.

On the title page of Dover reprint of the complete and revised edition of Thompson's book there is a beautiful illustration / photograph of spiral in the shell of Nautilus. That gave me an inspiration for Chapter IV of my book >> "Problem of the observer" which features D'Arcy Wentworth Thompson as its main character. Specially for the readers of the "Construction of Reality", I offer >> a download of an English translation of that chapter. The illustration on the image below also belongs to that chapter. The quote below the illustration is from the book and I think it is interesting in the context of the physical necessity and mathematics of shape which Thompson often discusses.

“A beautiful piece of evolution. A living fossil. But how was it made … And so regularly. Where does this mathematics come from, the logarithmic spiral? It is strange. In this spiral shell one can see the phenomenon of growth in its full mathematical simplicity, undisturbed by ephemeral effects. And the spiral is above life. It is some sort of principle, rational and mathematical cornerstone of life and universe. Because the same spiral pattern can be found in different species, in various sorts of gastropods and cephalopods. And even outside the phylum of mollusks, among ameboid foraminiferas, but also spirorbis, spirographis and ditrupa worms. And not only here and today … But millions of years before. In ammonite fossils. And even these inconspicuous Buccini hide the formula of ubiquitous spiral design, only a modest one. It is not only about evolution, it is about something much deeper. About the inevitability of shape and the connectedness of all living and non-living. Because, both living and non-living must obey the same laws of physics. And the laws of physics are mathematical. Yes, that is why it is so. Yes...”
Thompson was now contently nodding his head. Although, something was missing in all that.
“But… What does it mean that life is ordered in accordance with mathematical and physical laws? Does it mean that behind the universe there is a mind similar to ours whose intentions we can thus comprehend, or that mathematics and physics are nothing more but the best way to most easily fit the huge diversity of the universe in the material architecture of human brain? Perhaps it is only a miserable and impure resonant sound of a poorly tuned instrument, a sound we call mathematics. Mathematics as a resonance of this grey brain matter which, outside that matter, has a quite modest and restricted meaning. The way in which we describe not nature as it is, but only our knowledge of it... Does mathematician or nature itself introduces mathematics in the natural philosophy? In the end ... it is not that important. Science should, following the best example of physics, seek answers to big questions and theories that do not explain only the particular, but which bridge large distances and connect apparently completely different. Because the quality of science is measured by the extent of its relation to mathematics. And even if we in the end conclude that we stare in ourselves, it was worth a try. There is no use whatsoever in giving names to things.”

The spiral as the basic design element of seashells is not always obvious as in the case of Nautilus. One can also see it
from Haeckel's illustration of >> Prosobranchia on the image
above. Instead of seeking the formula that describes a shell it is much more useful, and more physically correct to code an
effective algorithm of shell growth. The original illustrations that I present in this post are a result of the coding of
one such algorithm (in PovRay).
As an alternative to seeking an equation for the seashell surface, the seashell can be represented as a sequence of the
objects in space, i.e. spheres and cylinders that were brought in their mutual spatial relations by the (time-dependent)
process of growth. But, such objects are still a discrete set so they need to be "fitted", "joined" in a single, smooth
object of the seashell. In the computer graphics there are objects especially suited for such purposes: metaballs or
blobs. The idea is to assign to each point in space (e.g. to each center of a sphere) a scalar field that
decays with the distance from the center. The total field of the set of points is a sum of all individual field and the
blob object is an iso-surface of such a field, i.e. a (hyper)surface with a prescribed magnitude of the total field.
The details of metaballs construction can be found in the paper by James Blinn [6]. I used this method in a recent
paper written together with my coauthors Anže Lošdorfer Božič and Rudi Podgornik. You can
>> download this paper from the arXiv (Energies and pressures in viruses: contribution of nonspecific
electrostatic interactions). We wanted to show a distribution of charge in virus coatings, but as the charges are discrete,
a set of points in 3D does not give the best insight in the charge distribution. For the purpose of clearer insight, we used
blobs in PovRay implementation.

Let's get back to seashells. Once we code the process of growth and we determine the way to connect the discrete set of points (blobs), what remains is to test the algorithm. Of course, one may try to create some "real" seashell, i.e. to fit the parameters of the algorithm until one gets a good agreement with the existing structure. That is the essence of many earlier works on mathematical construction of seashells (see e.g. [4]), and one such an attempt of mine is shown in the image above.
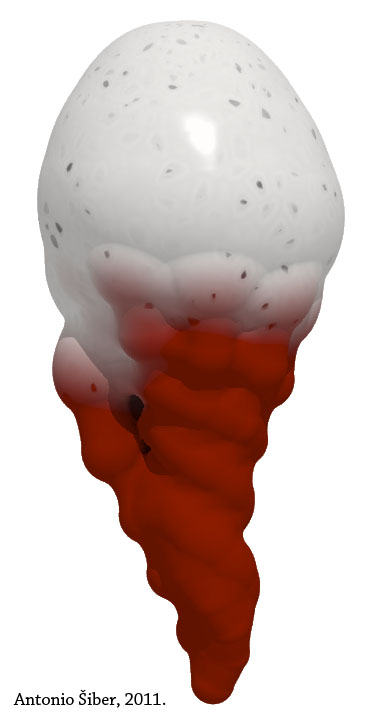
But, once you code "reality", really, there is no need to stick to one of its realizations. Let us construct (alternative) reality! The "seashell" above is an interesting construction based on an "algorithm for seashells", but completely unrelated to some "real" seashell. My two-year-old nephew did not recognize it as a seashell or a snail, and she nicely explained to me that it is an icecream! Seashell-icecream.
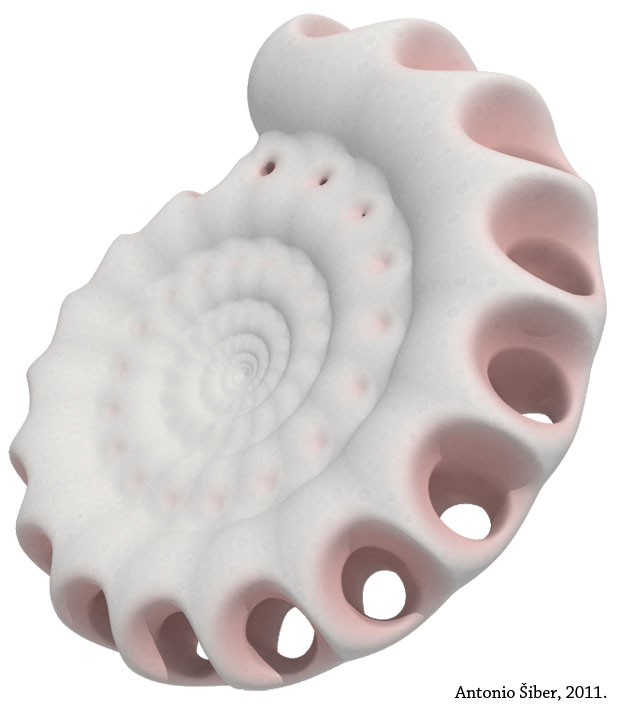
On the image above, I show another construction that looks a bit like an ammonite, but it is interesting due to additional elements, openings on the seashell structure. Imagine this image printed in a 150 x 150 cm size and set up over a fireplace. The pink color could be easily changed to yellowish or greenish, or even blue, in tune with other elements of the design in an imaginary living room.
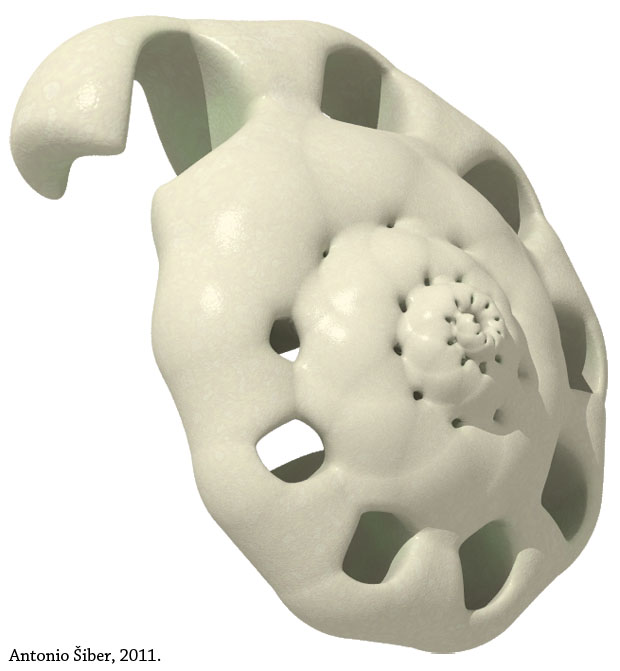

A similar, yet slightly different construction is shown on the image above. It is the same "seashell" viewed from above and below.

The image above contains probably the most unusual and the most difficult to recognize seashell that I constructed.
My nephew Ivor saw a "pebble" in it, but an algorithm that is behind the construction of this object is the same as
the one used to produce an image that opened this post, i.e. an easily recognizable snail.
And, in the end, I want to remind you in case you forgot:
1) >> HERE you can download the fourth chapter of "Problem of the observer", and
2) >> THIS link leads to a recently finished work regarding electrostatics of viruses on the arXiv.
LITERATURE :
[1] K. Jirapong and R.W. Krawczyk, Seashell Architectures, ISAMA/Bridges 2003 Conference, Mathematical Connections in
Art, Music, and Science, Granada University, Spain, July, 2003.
[2] J. Picado, Seashells: The plainness and beauty of their matehmatical description, Loci (March 2009),
DOI: 10.4169/loci003294
[3] D.R. Fowler, Hans Meinhardt and Przemyslaw Prusinkiewicz, Modeling seashells, SIGGRAPH '92, Proceedings of
the 19th annual conference on Computer graphics and interactive techniques, ACM New York, NY, USA, 1992
[4] C. Galbraith, P. Prusinkiewicz and B. Wyvill, Modeling Murex Cabritii Sea Shell with a Structured Implicit Surface,
CGI '00, Proceedings of the International Conference on Computer Graphics IEEE Computer Society Washington, DC, USA, 2000.
[5] C. Illert, Formulation and Solution of the Classical Seashell Problem. II Tubular Three-Dimensional Seashell Surfaces,
Il Nuovo Cimento 11 D (5), 761 (1989).
[6] J.F. Blinn, A Generalization of Algebraic Surface Drawing, ACM Transaction on Graphics, 1 (3), 235 (1982).
| << Music for bananas | Bruno Paun's caustic >> |
Last updated on 19th of September 2011.